Written by LeeKH

About the Markov Decision Process(MDP)¶

1. introduction¶

Reinforcement Learning의 이론적 기반을 이루고 있다
가장 간단한 경우의 MDP를 Markov Process(MP)라고 부른다
MP에 보상(reward)의 개념을 추가하면 Markov Reward Process 라고 부른다
여기에 행동(action)의 개념을 추가하면 Markov Decision Processes(MDPs)로 불리게 된다
MDP는 컴퓨터 과학 분야 뿐만 아니라 다른 영역에서도 활발히 사용된다. 이는 MDP를 기본으로 하는 RL을 다양한 분야에 적용할 수 있는 이유이기도 하다

가장 심플한 형태의 MDPs를 Markov Process 또는 Markov Chain이라고 함
어떤 시스템이 존재하고 그것을 관측 할 수 있다면 이를 상태(state)라고 한다
상태(state)의 집합, 모든 가능한 상태들을 State Space라고 부른다
State Space는 유한해야한다. 단, 그 크기가 계산할 수 없을 만큼 클 수는 있다
Observation은 관측되는 상태들을 의미하며 상태(state)의 리스트 혹은 나열로서 표현된다(sequence of states, chain). 이것이 Markov Process 혹은 Markov Chain으로 불리는 이유이다
이러한 Observation들의 리스트, 시퀀스를 강화학습(RL)에서는 history라고 부른다
특정 시스템이 Markov Process로 불리기 위해서는,
- Markov Property를 만족해야한다
- 이는 시스템의 다음 상태를 결정하기 위해서 필요한것이 오직 상태(state)뿐인 경우를 의미함
각 상태와 상태로 이동할 수 있는 확률(Transition Probabilities)들로 구성된다

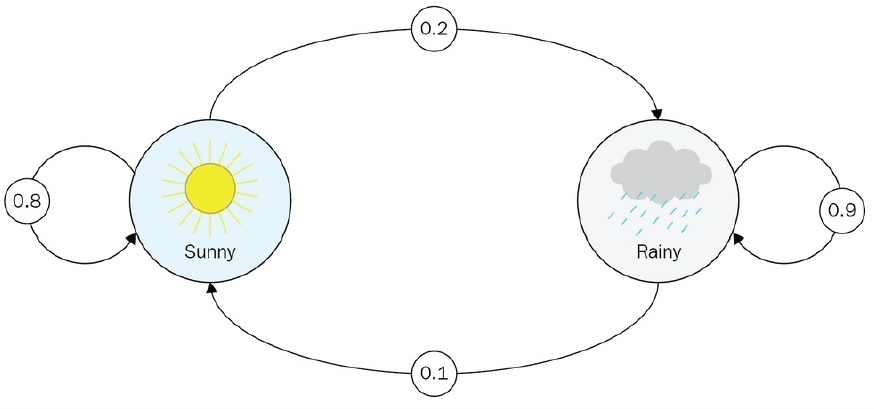
_images/1549519675522.png

위 그림이 대표적인 Markov Process이다. 날씨를 예측하는 아주 간략한 모델이다. 고려되는 것은 현재 상태의 날씨 뿐이며 현재 날씨에서 다음 날씨로 변동되는 상태 이동 확률을 기반으로 상태가 변경된다
만약 상태 이동 확률(probability of transition)이 0이면 edge를 그릴 필요는 없다
MP에서는 각 상태(state)들을 정의하고, 관측(observation)된 정보들(history)을 바탕으로 상태이동확률(transition prob.)을 계산하는 것으로 위의 그림과 같은 Markov Process(Markov Chain)을 구성하게 된다

해당 모델은 Markov Process에서 보상(Reward)의 개념이 추가된 버전이다
상태(state)에서 다른 상태로 이동(transition)하는 경우에 보상이 주어지는 것으로 볼 수 있다
Transition Matrix(가능한 모든 상태 이동 확률을 기록한 테이블)와 같은 크기로 확률 대신 보상을 기입한 테이블을 갖는다
보상의 개념과 함께 오는 것은 discount factor $\gamma$ 이다. 0과 1사이의 값이며 미래의 보상을 계산할때 사용되는 상수다
MRP는 MP에서 확장된 개념이므로 여전히 상태 이동 기록들을 관측(observe a chain of state transitions)하게 된다. MP에서는 이를 확률 계산에만 사용하면되지만 보상의 개념이 추가된 MRP에서는 이 history를 바탕으로 전체 보상인 return을 계산하게 된다
한번의 return이 주어지는 history를 episode라고 한다

$$ G_{t} = R_{t+1} + \gamma R_{t+2} + … = \sum_{k=0}^\infty\gamma^{k}R_{t+k+1} $$

return의 의미는 현재 상태에서 받는 보상과는 개념이 다소 다르다. 이는 미래에 받게될 보상의 기대치로 생각을 할 수 있다. 미래의 보상에 감소율인 $\gamma$를 계속 곱해 너무 멀리 바라보거나($\gamma = 1$), 당장의 보상만 바라보는($\gamma = 0$) 중간의 정도를 계산하는 수식을 (1)에서 보여주고 있다
강화학습에서 $\gamma$(discount factor)를 간단히 설명하사면, agent가 이후의 보상을 고려할 경우 미래를 어느정도 보고 결정할 것인지에 대한 상수 값으로 볼 수 있다
Value of State, 상태에 대한 가치 값이라고 불리는 값은 곧 무수히 많이 수집된 chain들(관측 결과들)을 바탕으로하는 기대치로 정의할 수 있다 $$ V(s) = E[G|S_{t} = s] $$
수식(2)가 의미하는 바는 간단하다. 모든 상태 s에 대해서 얻게되는 return값인 G들의 평균 혹은 기대값을 곧 상태의 가치(Value of State)로 정의하는 것이다
$\gamma$의 값을 0으로 하는 것과 1로 하는 것 또는 그 사이의 값으로 결정하는 요인은 각 환경마다 다르다고 볼 수 있다

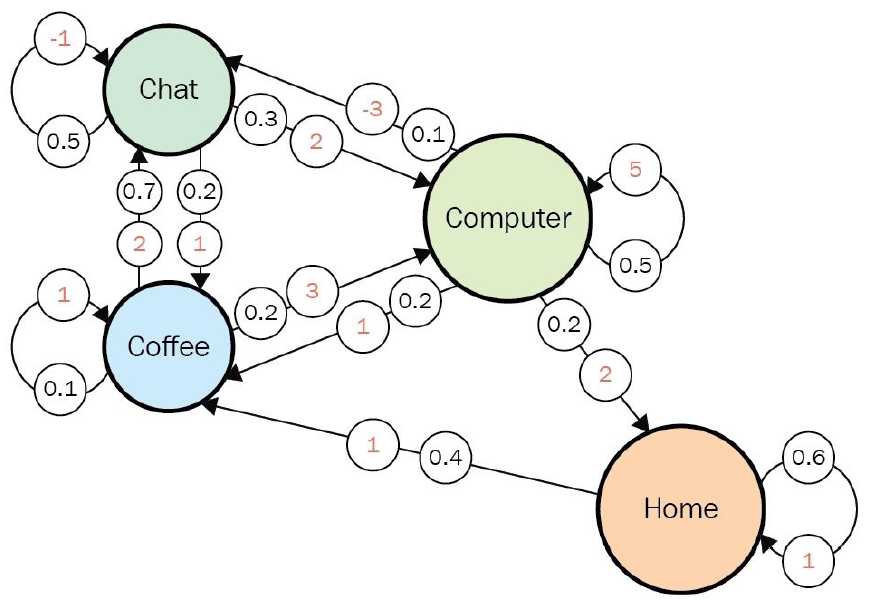
_images/1549523256201.png

위 그림은 Dilbert Reward Process이다. 이 경우 $\gamma$의 값이 0이면 각 state에서 얻을 수 있는 즉각적인 보상에만 집중하게 될 것이고 $\gamma$의 값이 1이 되면 미래의 보상을 계산하기 위해 무한히 transition을 수행해야한다. 이러한 예시의 경우에는 0과 1사이의 값을 적절히 선택해야할 필요가 있다

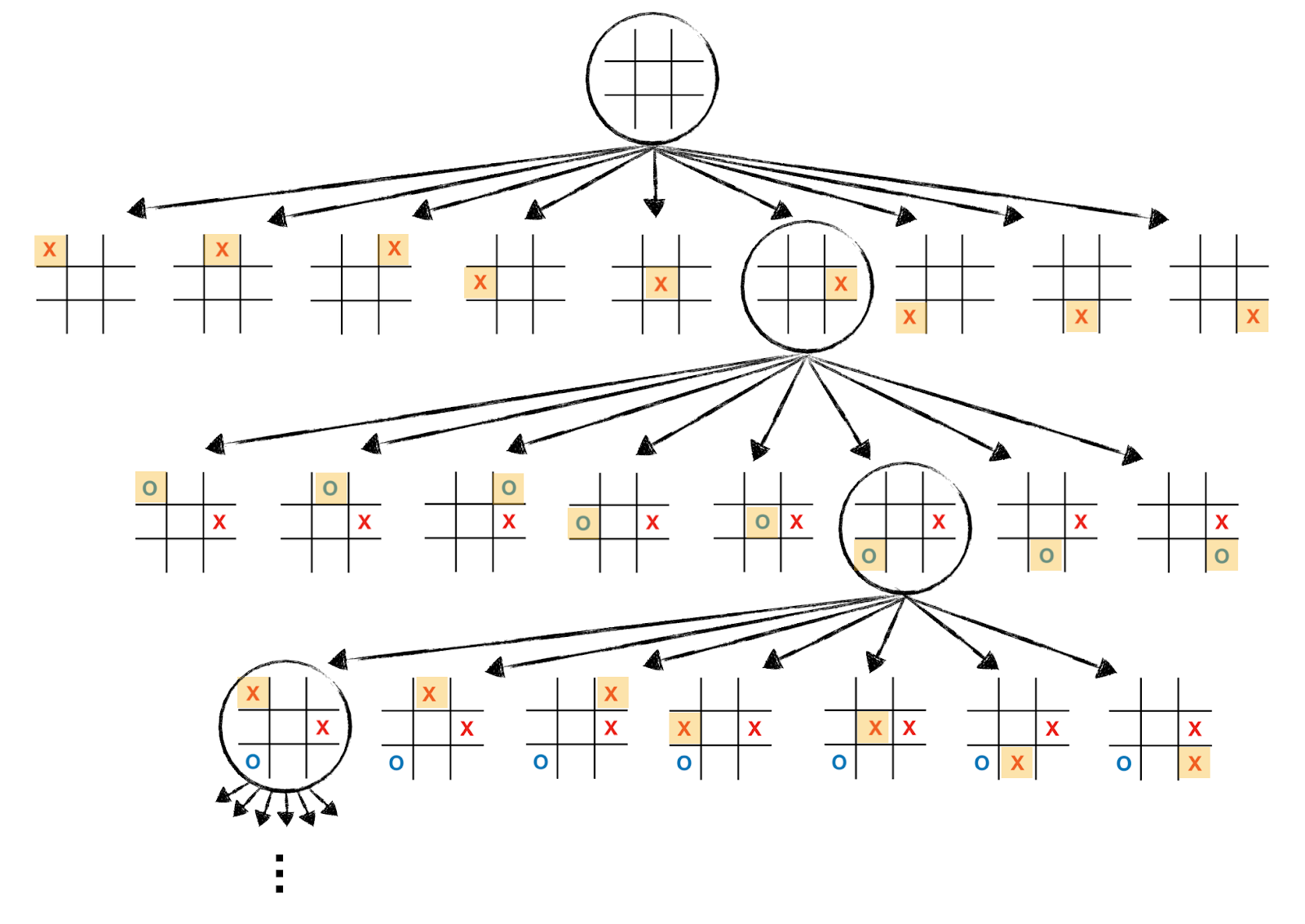
_images/0_SUA-USjrmMfHKf2Q_.png

위 그림은 Tic-Tac-Toe 게임의 과정을 보여주고 있다. 틱택토는 보통 9번의 state변화 이후 게임이 종료되는데, 이러한 환경을 finite-horizon environment라고 정의하고 있다. 이런 문제의 경우 $\gamma$를 1로 해도 상관이 없다. 오히려 좋다

_images/96-4.jpg

다른 예시로 Multi-Armed Bandit MDP가 있다. 이 예시에 대한 자세한 설명은 생략하고 핵심만 말하자면 한번의 슬롯을 당기는 것으로 하나의 episode가 끝이난다. 이러한 경우에는 $\gamma$를 0으로 설정하게 될 것이다

해당 모델은 Markov Reward Process에서 행동(Action)의 개념이 추가된 버전이다
모든 행동들의 집합을 agent의 action space라고 한다. Action의 개수는 유한해야 한다
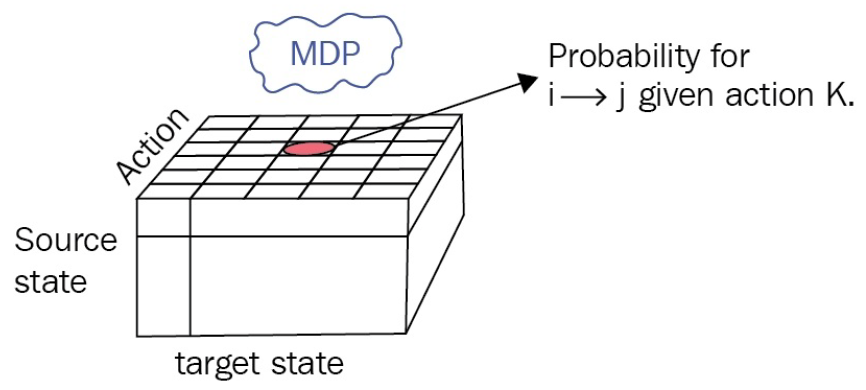
MPs(Markov Processes)와 MRPs(Markov Reward Processes)에서 고려되던 transition probability matrix는 action 개념이 추가되면서 큐브형태의 transition probabilities for MDP를 위 그림처럼 생각해 볼 수 있다

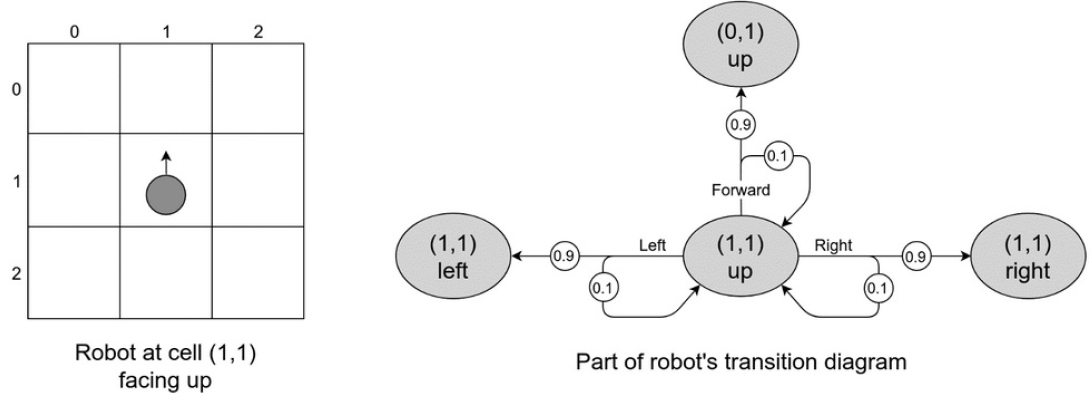
_images/1549525475596.png

Agent를 로봇이고 그 로봇은 불완전한 엔진을 갖고 있어 방향 전환에 성공할 확률을 갖고 있다고 생각 해 볼 수 있다. 이는 행동을 선택하는 것에도 확률이 들어가게 되는 것이다
위 그림은 GridWorld위 (1,1)에 있는 로봇이 행동 할 수 있는 모든 다음 상태들을 action probabilities과 함께 표시한 다이어그램이다
RL과 MDPs를 수식으로 정의하는데 있어 핵심적으로 다뤄지는 것이 정책(policy)이다
정책(policy)은 agent의 행동을 결정하는 규칙으로서 작동한다
강화학습의 목표는 최적의 정책(optimal policy, $\pi^{*}$)을 찾아 더 많은 return을 얻는 것이다. 정책에 따라 agent는 행동을 수행하기 때문에 정책에 따라 return의 값이 역시달라진다고 볼 수 있다. 따라서 정책의 개념(notion of policy)을 결정하는 것은 매우 중요하다.

$$ \pi(a|s) = P[A_{t}=a|S_{t}=s] $$

수식으로 보자면, 정책은 모든 가능한 상태들에 대한 행동의 확률 분포로 볼 수 있다. 보다시피 행동은 고정된 값이 아닌 무작위성을 지닌 확률 값으로 결정된다.
확률적 행동 접근은 무작위성 탐색폭을 가능하게 함으로서 더 나은 정책을 찾는데 도움을 주게 된다
만약 정책의 값이 변화하지 않고 고정된 값이라면, MDP는 곧 MRP로 볼 수 있다