Written by LeeKH

Why we use the Q-function?

Value of state & Value of action

이전 글에서는 Bellman equation을 바탕으로 모든 행동들에 대한 가치 $V$를 계산하는 방법으로 최적 정책을 찾아 나갔다. 그 경우 가치 함수 $V$가 입력으로 받는 것은 상태 $s$뿐이다. 이번 글에서는 상태 $s$와 특정 행동 $a$를 입력으로 받아 그 가치를 계산하는 $Q$함수를 정의한다.

$$ Q_{s,a} = \mathbb{E}{s’\sim S}[r{s,a} + \gamma V_{s’}] = \sum_{s’ \in S}p_{a,s\to s’}(r_{s,a} + \gamma V_{s’}) $$

특정 행동과 상태를 고려하는 가치함수인 Q함수를 이용한 방법을 Q-Learning 이라고 한다. Q함수에 대한 수식과정을 살펴보면 이전의 가치함수, 벨만 방정식과 비슷한데 굳이 Q함수를 사용하는 이유는 실제 적용시의 편리함 때문이다. Value of state $V_s$를 Q함수로 표현하면,

$$ V_s = \max_{a\in A}Q_{s,a} $$

즉 현재 상태에서의 최대 기대값이란, 현재 상태에서 할 수 있는 모든 행동들 각각의 기대값 중 가장 큰 값을 의미한다. $Q(s,a)$로 Q함수를 아래와 같이 recursive하게 정의하고 이후 Q-learning에 사용된다.

$$ Q(s,a) = r_{s,a} + \gamma \max_{a’ \in A}Q(s’, a’) $$

Q-function with simple example

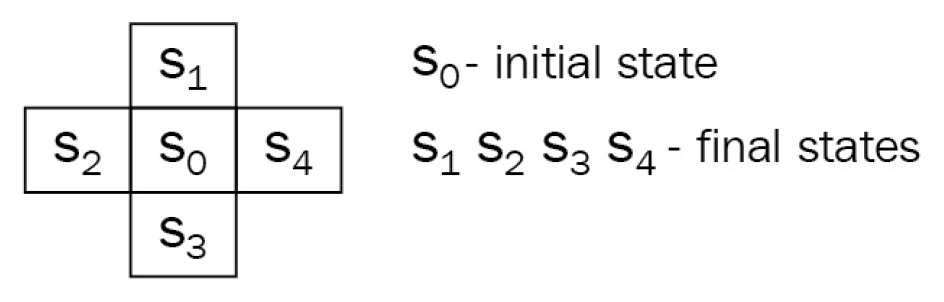
• 초기 상태 $S_{0}$에서 항상 시작한다
• 다음 상태는 $S_{1,2,3,4}$뿐이며 해당 상태들에서 episode가 종료된다
• Agent는 위, 아래, 왼쪽, 오른쪽 총 4가지의 행동을 갖는다
• 각 행동은 확률적이며 원래 가려던 방향으로 이동, 왼쪽이나 오른쪽으로 미끄러질 가능성이 모두 동일하다고 하자. 그렇다면 아래 그림과 같은 상태 이동 확률이 추가된 다이어그램으로 example을 설명할 수 있다

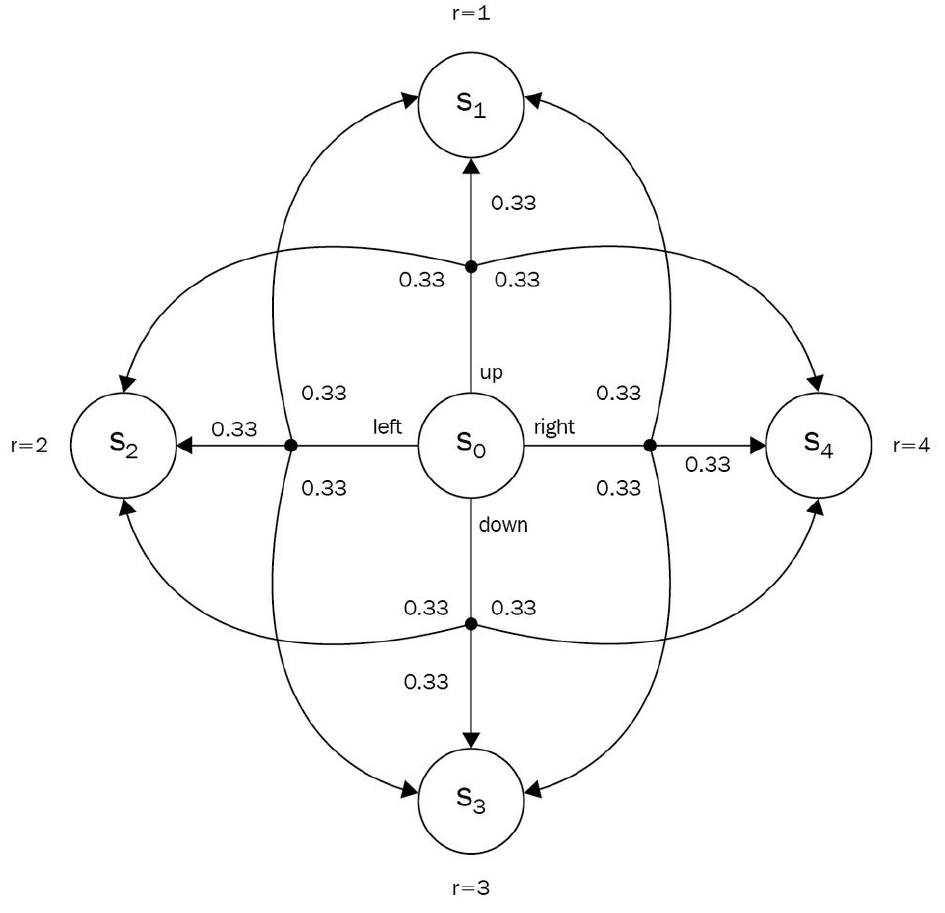
• $S_{0}​$에서 $S_{1,2,3,4}​$이후의 상태는 없으므로 $S_{1,2,3,4}​$에서의 보상은 각 상태의 immediate reward값인 $r​$에 해당한다(위의 예시가 간단한 이유). $V_{1,2,3,4} = r_{1,2,3,4}​$
• $Q(s_0, left) = 0.33 \cdot V_1 + 0.33 \cdot V_2 + 0.33 \cdot V_3 = 0.33 \cdot 1 + 0.33 \cdot 2 + 0.33 \cdot 3​$

위와 같은 방식으로 Q함수 값을 계산 가능하다. 그리고 실제로 적용하기에도 훨씬 편리하다. 아래 두 수식을 살펴보자.

Q함수를 사용한다면 다음 행동 $a’$을 결정하기 위해 할 일은 그저 가장 큰 Q값에 해당하는 행동을 고르는 것이다.

$$ a’ = argmax_{a \in A}Q(s, a) $$

반면에 value of states $V_s$를 사용하는 경우는,

$$ a’ = argmax_{a \in A}\mathbb{E}{s \sim S}[r{s,a}+\gamma V_s]=argmax_{a\in A}\sum_{s\in S}p_{a,0\to s}(r_{s,a}+\gamma V_s) $$

위 수식에서 보여지듯이 상태 이동 확률과 각 상태의 가치 모두 알아야 한다.

실제 학습 과정에서 각 상태의 가치나, 상태 이동 확률을 사전에 모두 파악하는 것은 매우 힘들다. 따라서 이를 고려하지 않는 Q함수를 사용하는것이 바람직하다

References

• Deep Reinforcement Learning Hands-On, Maxim Lapan, 2018