Written by LeeKH
The Bellman equation of optimality¶
Bellman equation with deterministic example¶
Bellman equation을 살펴보기 위해 아래 간단한 예시부터 살펴본다.
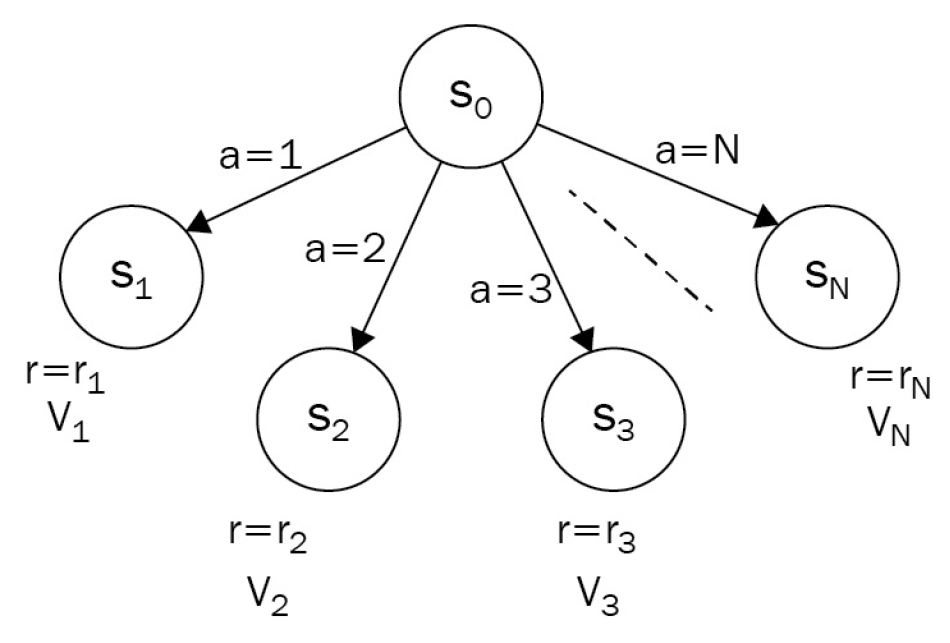
시작 상태 $S_{0}$에서 항상 시작한다
모든 행동은 100% 보장된다
다음 상태 $S_{1…N}$에 대해서 각 상태의 보상 $r_{1…N}$을 알고있다고 가정한다
다음 상태 $S_{1 … N}$에 대해서 각 상태의 가치 $V_{1…N}$을 알 수 있다고 가정한다
다음 상태의 가치는 $V_{0}(a = a_{i}) = r_{i} + V_{i}$ 와 같이 계산한다
Agent는 가장 가치있는 행동을 하기위해 가능한 모든 행동에서 얻어지는 가치를 계산한다
$$ V_{0} = max_{a\in 1…N}(r_{a} + V_{a}) $$
여기에 discount factor $\gamma$를 고려하는 경우
$$ V_{0} = max_{a\in 1…N}(r_{a} + \gamma V_{a}) $$
위의 예시에서는 Agent가 Greedy하게 행동하기 때문에 즉각적인 보상에 집중해 행동하는 것 처럼 보인다. 다음 행동에 대한 가치 $V$와 즉각적인 보상인 $\gamma$를 합쳐 가장 큰 값을 주는 행동을 취하기 때문이다. 하지만 가치 $V$가 장기적 행동에 따른 보상을 의미하기 때문에 실제로는 눈 앞의 이익만을 쫓는 행동을 한다는 것은 틀린 이야기다
위의 식과 같이 다음 가치를 고려하며 행동을 결정하는 행위가 optimal이 된다는 것을 Richard Bellman이 증명하였다. 앞서 소개한 식이 바로 Bellman Equation of Value이며 deterministic한 경우만 고려한다. 그렇다면 각 행동(action)이 확률적인(stochastic) 경우 어떻게 해야하는가?
Bellman equation with stochastic example¶
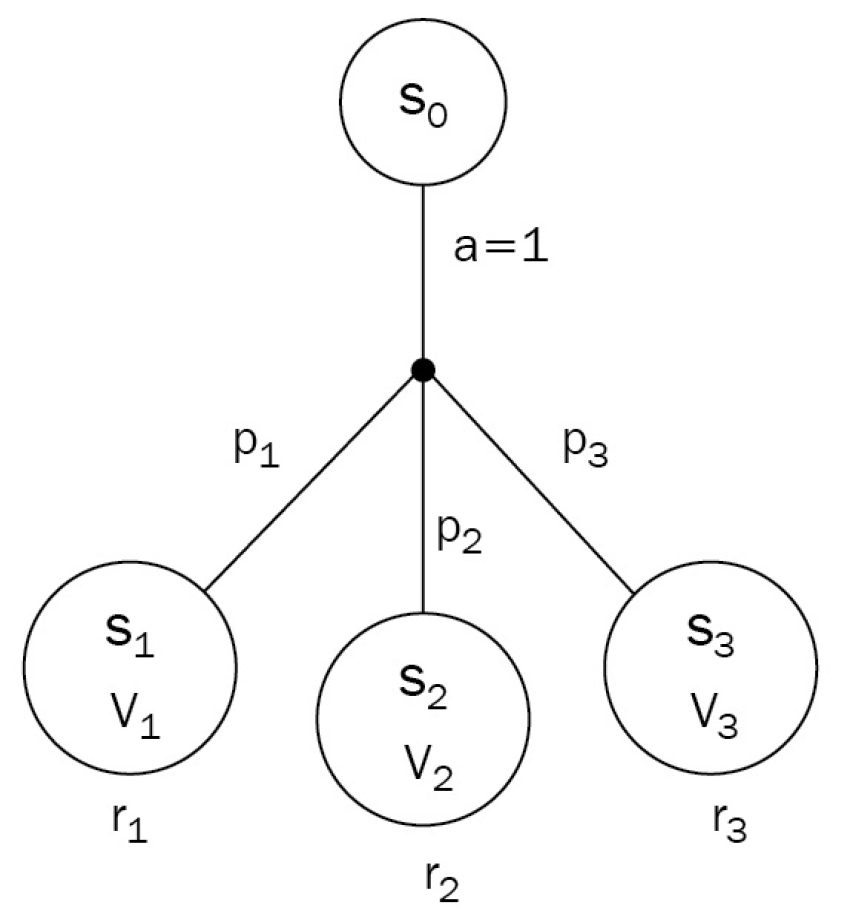
- 위 그림에서 초기 상태 $S_{0}$에서 Agent는 행동 $a$를 수행한다
- 다음 상태 $S_{1,2,3}$은 각각 보상 $r_{1,2,3}$과 가치 $V_{1,2,3}$을 갖고 각 상태로 이동할 확률 $p_{1,2,3}$을 갖는다
- $p_{1} + p_{2} + p_{3} = 1$을 만족한다
- 이처럼 상태 이동 확률을 갖는 stochastic한 경우에 대해 Bellman Equation은 아래와 같다
$$ V_{0} = p_1(r_1 + \gamma V_1) + p_2(r_2 + \gamma V_2) + p_3(r_3 + \gamma V_3) $$
- 위 수식을 일반적인 수식으로 표현하면 아래와 같다
$$ V_{0}(a) = \mathbb{E}{s \sim S}[r{s,a} + \gamma V_s] = \sum_{s \in S}^{} p_{a,0 \to s}(r_{s,a} + \gamma V_s) $$
- 하나의 확률적 행동 $a$에 대한 기대값을 위와 같이 계산할 수 있다. 이제 최적의 행동을 선택하기 위해 deterministic case의 Bellman Equation을 합치면 아래 수식과 같다
$$ V_{0}=\max_{a \in A}\mathbb{E}{s \sim S}[r{s,a}+\gamma V_s]=\max_{a\in A}\sum_{s\in S}p_{a,0\to s}(r_{s,a}+\gamma V_s) $$
위 수식을 좀 더 자세히 살펴보자. $V_0$값은 초기 상태 $S_0$에서 할 수 있는 모든 행동 $a \in A$에 대해 기대값이 최고로 높은 하나의 행동 $a^{}$의 기대값을 의미한다. Agent는 당연히 $a^{}$에 해당하는 행동을 수행 할 것이다.
Deterministic한 경우와 다르게 행동 1개가 다음 상태 1개로 대응되지 않고 확률적으로 여러 상태와 물려있기 때문에 이를 전부 고려한다. 각 상태들의 기대값에 대한 비율은 상태 이동 확률 $p_{a,0 \to s}$을 사용한다. 상태 이동 확률로 곱해지는 각 상태의 기대값은 장기적 보상 기대치와 discount factor $\gamma$가 곱해진 $\gamma V_s$과 즉각적인 보상 $r_{s,a}$의 합으로 얻어진다.
이처럼 하나의 행동 $a$ 에서 수행 가능한 상태 $s \in S$의 모든 가치들의 합을 상태 이동 확률비로 합치면 행동 $a$에 대한 $V_{0}$의 기대값 $V_{0}(a)$를 얻을 수 있고 이를 모든 행동 $a \in A$에 대해 수행하여 최대 값을 구한다
Conclusion¶
Bellman equation은 이처럼 강화학습에서도 사용되지만 일반적인 동적 프로그래밍(Dynamic programming)분야에도 널리 적용된다. 또한 강화학습에서는 최고의 보상값을 계산해주는 방법으로 사용됨과 동시에 최적의 정책(policy)을 주기도 한다. 이것이 가능한 이유는 Bellman의 optimality 증명 덕분인데, 이는 하나의 step이 완료될 경우 즉각적인 보상과 감소율이 적용된 장기적 보상 수치의 합이 최대인 행동만 선택하는 것이 가장 optimal 하다는 내용이다.
Reference¶
- Deep Reinforcement Learning Hands-On, Maxim Lapan, 2018